Решение иррациональных уравнений методом оценки
Одним из методов решения иррациональных уравнений является метод оценки. В этой статье сначала мы всесторонне разберем, в каких случаях и каким образом иррациональные уравнения решаются методом оценки. А после этого рассмотрим решения большого количества характерных иррациональных уравнений.
Для решения каких иррациональных уравнений используется метод оценки?
Метод оценки - это одно из направлений функционально-графического метода решения уравнений. А функционально-графический метод обычно используется тогда, когда другие методы не позволяют получить решение. Значит, к методу оценки стоит прибегать лишь тогда, когда нет возможности решить иррациональное уравнение другими более привычными и простыми методами.
Следующим по значимости признаком, склоняющим к использованию метода оценки для решения заданного иррационального уравнения, является очевидная или довольно отчетливо просматривающая возможность получения оценок значений выражений (или оценок значений соответствующих функций), отвечающих частям уравнения.
Дальше нужно смотреть на полученные оценки. Дело в том, что не все оценки позволяют продвинуться в решении заданного уравнения. Подробнее о том, какие оценки позволяют получить решение уравнения, речь пойдет в одном из следующих пунктов.
Итак, к методу оценки для решения иррационального уравнения целесообразно обращаться, если
- не видно более простого метода решения,
- есть возможность оценить значения выражений, отвечающих частям уравнения,
- полученные оценки позволяют продвинуться в решении.
Вспоминаем суть метода
Суть метода оценки состоит в использовании оценок значений частей уравнения для перехода к равносильной системе уравнений или для обоснования отсутствия корней.
Из этого понятно, что решение уравнений методом оценки проводится в два этапа. Первый этап – это оценка значений функции y=f(x) (или соответствующего выражения f(x), что по сути одно и то же), если решается уравнение f(x)=C, или оценка значений функций y=g(x) и y=h(x) (или соответствующих выражений f(x) и g(x)), если решается уравнение g(x)=h(x). Второй этап – это использование полученных оценок для дальнейшего поиска корней уравнения или обоснования их отсутствия.
Как оцениваются значения выражений?
Этот вопрос детально разобран в отдельной статье Как оценить значения выражения (функции). Здесь мы ограничимся перечислением способов оценки, которые наиболее часто используются при решении методом оценки именно иррациональных уравнений. Вот этот список способов оценки:
-
Оценка на основании определения корня с четным показателем. Так как по определению корень с четным показателем есть неотрицательное число, то для любого x из ОДЗ для выражения
 , где n – натуральное число, p(x) – некоторое выражение, справедливо неравенство
, где n – натуральное число, p(x) – некоторое выражение, справедливо неравенство  , причем
, причем  тогда и только тогда, когда p(x)=0.
тогда и только тогда, когда p(x)=0.
-
Оценка на основании следующего свойства корней: для любых неотрицательных чисел a и b, a<b (≤, >, ≥), выполняется неравенство
 (≤, >, ≥). Если для любого x из ОДЗ для выражения
(≤, >, ≥). Если для любого x из ОДЗ для выражения  выполняется неравенство p(x)<c (≤, >, ≥), где c – некоторое неотрицательное число, то для любого x из ОДЗ справедливо неравенство
выполняется неравенство p(x)<c (≤, >, ≥), где c – некоторое неотрицательное число, то для любого x из ОДЗ справедливо неравенство  (≤, >, ≥).
(≤, >, ≥).
- Оценка на базе того факта, что степень любого числа с четным показателем есть неотрицательное число. Для любого x из ОДЗ для выражения p2·n(x) справедливо неравенство p2·n(x)≥0, причем p2·n(x)=0 тогда и только тогда, когда p(x)=0.
-
Оценка значений квадратного трехчлена. Для оценки можно использовать ординату вершины параболы, и при отрицательном дискриминанте - ноль.
- Если a>0, то a·x2+b·x+c≥y0, где y0 – ордината вершины параболы, а если a<0, то a·x2+b·x+c≤y0.
- Если a>0 и дискриминант D<0, то a·x2+b·x+c>0, а если a<0 и D<0, то a·x2+b·x+c<0.
-
Оценка на базе свойств числовых неравенств.
- Если на множестве X выполняется условие p(x)<B (≤, >, ≥), где B – некоторое число, то для любого числа C на множестве X будет справедливо неравенство p(x)+C<B+C (≤, >, ≥). Равенство возможно тогда и только тогда, когда p(x)=B.
-
Если на множестве X выполняется условие p(x)<B (≤, >, ≥), где B – некоторое число, то на множестве X для любого положительного числа C будет справедливо неравенство C·p(x)<C·B (≤, >, ≥), а для любого отрицательного C – неравенство C·p(x)>C·B (≥, <, ≤). Равенство возможно тогда и только тогда, когда p(x)=B.
Следствие. Если на множестве X выполняется условие p(x)<B (≤, >, ≥), где B – некоторое число, то на X справедливо неравенство -p(x)>-B (≥, <, ≤). Равенство возможно тогда и только тогда, когда p(x)=B. -
Если на множестве X значения выражения p(x) положительные и выполняется условие p(x)<B (≤, >, ≥), где B – некоторое положительное число, то на X будет справедливо неравенство
 (≥, <, ≤).
(≥, <, ≤).
- Если на множестве X выполняется условие p1(x)<B1, p2(x)<B2, …, pn(x)<Bn (≤, >, ≥), где B1, B2, …, Bn – некоторые числа, то на множестве X справедливо неравенство p1(x)+p2(x)+…+pn(x)<B1+B2+…+Bn (≤, >, ≥). Равенство возможно тогда и только тогда, когда одновременно p1(x)=B1, p2(x)=B2, …, pn(x)=Bn.
-
Если на множестве X все значения всех выражений p1(x), p2(x), …, pn(x) являются положительными числами и выполняются все условия p1(x)<B1, p2(x)<B2, …, pn(x)<Bn (≤, >, ≥), где B1, B2, …, Bn – некоторые положительные числа, то на множестве X справедливо неравенство p1(x)·p2(x)·…·pn(x)<B1·B2·…·Bn (≤, >, ≥). Равенство возможно тогда и только тогда, когда одновременно p1(x)=B1, p2(x)=B2, …, pn(x)=Bn.
Следствие. Если на множестве X все значения выражения p(x) есть положительные числа и выполняется условие p(x)<B (≤, >, ≥), где B – некоторое положительное число, то на множестве X справедливо неравенство pn(x)<Bn (≤, >, ≥). Равенство возможно тогда и только тогда, когда p(x)=B.
- Оценка через наибольшее и наименьшее значение функции, найденное с использованием производной. Если A - наименьшее значение функции p на множестве X, то на X справедливо неравенство p(x)≥A. Если B - наибольшее значение функции p на множестве X, то на X справедливо неравенство p(x)≤B.
Как использовать полученные оценки?
Допустим, с первым этапом мы справились, то есть, оценили значения функций. Возникает логичный вопрос о том, как дальше использовать полученные оценки для решения уравнения. А дальше нужно сослаться на одно из следующих утверждений:
-
Уравнение f(x)=C не имеет решений на множестве X в следующих случаях:
- Если f(x)<A и A<C.
- Если f(x)≤A и A<C.
- Если f(x)>B и B>C.
- Если f(x)≥B и B>C.
- Если f(x)<C.
- Если f(x)>C.
-
Уравнение f(x)=C на множестве X равносильно системе уравнений
 в следующих случаях:
в следующих случаях:
- Если на множестве X f(x)≤C, причем f(x) представляет собой сумму функций f1(x), f2(x), …, fn(x) таких, что f1(x)≤C1, f2(x)≤C2, …, fn(x)≤Cn (при этом C1+C2+…+Cn=C).
- Если на множестве f(x)≥C, причем f(x) представляет собой сумму функций f1(x), f2(x), …, fn(x) таких, что f1(x)≥C1, f2(x)≥C2, …, fn(x)≥Cn (при этом C1+C2+…+Cn=C).
- Если на множестве X f(x)≤C, причем f(x) представляет собой произведение функций f1(x), f2(x), …, fn(x) таких, что 0≤f1(x)≤C1, 0≤f2(x)≤C2, …, 0≤fn(x)≤Cn (при этом C1·C2·…·Cn=C).
- Если на множестве X f(x)≤C, причем f(x) представляет собой произведение функций f1(x), f2(x), …, fn(x) таких, что f1(x)≥C1, f2(x)≥C2, …, fn(x)≥Cn, где числа C1, C2, …, Cn - неотрицательные (при этом C1·C2·…·Cn=C).
-
Уравнение g(x)=h(x) не имеет решений на множестве X в следующих случаях:
- Если g(x)<A, h(x)>B и A<B.
- Если g(x)≤A, h(x)>B и A<B.
- Если g(x)<A, h(x)≥B и A<B.
- Если g(x)≤A, h(x)≥B и A<B.
-
Уравнение g(x)=h(x) не имеет решений на множестве X и в следующих случаях:
- Если g(x)<C, h(x)>C.
- Если g(x)≤C, h(x)>C.
- Если g(x)<C, h(x)≥C.
-
Если на множестве X значения одной из функций g и h не меньше некоторого числа C, а значения другой функции не больше этого числа C, то уравнение g(x)=h(x) равносильно на множестве X системе
 .
.
Положения второго блока утверждений следуют из свойств сложения и умножения верных числовых неравенств одного смысла.
Первый блок положений становится понятен, если представить взаимное расположение графика функции f и прямой y=C, а положения остальных блоков – если представить взаимное расположение графиков функций g и h.
Разберем первый блок утверждений. Когда график функции f ниже или не выше прямой y=A, которая в свою очередь ниже прямой y=C, то понятно, что он не пересекается с прямой y=C, из этого вытекает отсутствие корней уравнения f(x)=C. Когда график функции f выше или не ниже прямой y=B, которая в свою очередь выше прямой y=C, то понятно, что он не пересекается с прямой y=C, из этого вытекает отсутствие корней уравнения f(x)=C. Когда график функции f ниже или выше прямой y=С, то понятно, что он не пересекается с этой прямой, из этого также вытекает отсутствие корней уравнения f(x)=C.
Теперь обоснуем третий блок утверждений. Пусть на множестве X значения функции g меньше или не больше числа A, а значения функции h больше или не меньше числа B. Это означает, что все точки графика функции g находятся ниже или не выше прямой y=A, а точки графика функции h – выше или не ниже прямой y=B. Понятно, что на множестве X при A<B графики функций g и h не будут иметь общих точек, так как график функции g будет расположен ниже графика функции h. А это означает, что уравнение g(x)=h(x) не имеет решений.
Переходим к четвертому блоку утверждений. Здесь в первом случае один график расположен ниже этой прямой, другой – выше этой прямой. Во втором случае один график не выше этой прямой, другой – выше этой прямой. В третьем случае один график ниже этой прямой, другой – не ниже этой прямой. Понятно, что во всех случаях графики не имеют общих точек, значит, уравнение g(x)=h(x) не имеет решений.
В последней ситуации график одной функции не выше прямой y=C, а график другой функции – не ниже этой прямой. При этом понятно, что графики могут иметь общие точки только на этой прямой. Это и объясняет переход от уравнения g(x)=h(x) к системе  .
.
Можно переходить к практике.
Примеры решения иррациональных уравнений
Рассмотрим решения характерных иррациональных уравнений методом оценки.
Для начала стоит разобраться с вопросом точности оценки значений выражений. Чтобы было понятно, откуда берется такой вопрос, посмотрите на три оценки значений корня  : первая
: первая  , вторая
, вторая  , третья
, третья  , и скажите, какую предпочесть? Ну, первую отбросим, так как она по большей части надумана, а вот вторая и третья оценки вполне рабочие, и в зависимости от ситуации может быть использована и первая из них, сравнительно грубая, и вторая. Посмотрим на этот вопрос с позиций практики.
, и скажите, какую предпочесть? Ну, первую отбросим, так как она по большей части надумана, а вот вторая и третья оценки вполне рабочие, и в зависимости от ситуации может быть использована и первая из них, сравнительно грубая, и вторая. Посмотрим на этот вопрос с позиций практики.
Для доказательства того, что уравнение не имеет решений, бывает достаточно грубых оценок. Основное преимущество грубых оценок перед более точными оценками состоит в относительной простоте их получения. Грубые оценки практически очевидны и не требуют дополнительных исследований, так как в их основе лежат хорошо известные факты, такие как: квадратный корень – это неотрицательное число, модуль – это неотрицательное число, квадрат числа – это неотрицательное число, сумма положительных взаимно обратных чисел не меньше двух, значения квадратного трехчлена с отрицательным старшим членом и отрицательным дискриминантом - отрицательные и т.п. Так для решения следующего иррационального уравнения методом оценки достаточно грубой оценки корня с одной стороны и квадратного трехчлена с другой стороны.
Обычно проще получить грубые оценки значений функций или выражений, чем точные. Но довольно часто грубые оценки не позволяют сделать выводы о корнях решаемых уравнений, в то время как более точные оценки дают такую возможность. Давайте решим типовое иррациональное уравнение.
Будем считать, что разобрались, когда применять грубые оценки, а когда более точные. Теперь перейдем к решению методом оценки иррациональных уравнений вида f(x)=C.
Начнем с решения простого, но очень характерного иррационального уравнения: оценка значений его левой части вытекает из оценок составляющих ее корней, и из полученной оценки следует вывод об отсутствии корней уравнения.
Интереснее обстоит дело, когда выражение, отвечающее левой части иррационального уравнения f(x)=C, представляет собой сумму или произведение нескольких выражений и его значения оцениваются как f(x)≤C или f(x)≥C. В таких случаях записанные выше утверждения предписывают переходить от исходного иррационального уравнения к равносильной системе уравнений. Приведем решение характерного иррационального уравнения.
Закрепим навыки перехода по методу оценки от иррационального уравнения f(x)=C с суммой или произведением в левой части к равносильной системе уравнений. Для этого решим сравнительно сложное иррациональное уравнение, левая часть которого представляет собой сумму двух иррациональных выражений, одно из которых является произведением двух выражений. Принцип решения тот же: получаем оценку, которая позволяет перейти от исходного уравнения к равносильной системе.
Перейдем к иррациональным уравнениям вида g(x)=h(x).
Предыдущие примеры были довольно простые в плане оценки значений выражений и функций. Пришло время проработать аспект оценки более детально. По понятным причинам упор сделаем на способах оценки, к которым приходится прибегать наиболее часто при решении методом оценки именно иррациональных уравнений. Начнем со способов оценки, не требующих нахождения производной. Так чтобы решить следующее иррациональное уравнение, придется привлечь чуть ли не все известные средства: от свойства степеней с четным показателем и свойства монотонности функции извлечения корня до оценок на базе свойств числовых равенств.
Способы получения оценок, которые мы использовали во всех предыдущих примерах, не закрывают вопрос оценки значений полностью. Другими словами, не всегда с их помощью удается оценить значения функций и выражений. В частности, рассмотренные способы нехороши, когда область допустимых значений переменной x для решаемого иррационального уравнения отлична от множества всех действительных чисел R. В качестве примера приведем оценку корня  в двух случаях: когда ОДЗ есть множество R и когда ОДЗ есть отрезок от 3 до 5. Опираясь на способы оценки, которыми мы пользовались выше, мы можем получить оценку
в двух случаях: когда ОДЗ есть множество R и когда ОДЗ есть отрезок от 3 до 5. Опираясь на способы оценки, которыми мы пользовались выше, мы можем получить оценку  . Для случая, когда ОДЗ есть множество R, эта оценка очень даже хороша. Но для случая, когда ОДЗ есть отрезок [3, 5], записанная оценка
. Для случая, когда ОДЗ есть множество R, эта оценка очень даже хороша. Но для случая, когда ОДЗ есть отрезок [3, 5], записанная оценка  уже оказывается сравнительно грубой, и есть возможность оценить корень более точно, а именно как
уже оказывается сравнительно грубой, и есть возможность оценить корень более точно, а именно как  . Но не только ОДЗ ограничивает возможности получения оценок разобранными выше способами. Часто эти способы не дают возможности оценить значения функции из-за вида оцениваемой функции. Например, способы оценки, о которых мы говорим, позволяют оценить значения корней
. Но не только ОДЗ ограничивает возможности получения оценок разобранными выше способами. Часто эти способы не дают возможности оценить значения функции из-за вида оцениваемой функции. Например, способы оценки, о которых мы говорим, позволяют оценить значения корней  и
и  , а также их сумму:
, а также их сумму:  ,
,  , откуда
, откуда  и дальше
и дальше  . Но эти способы оценки уже не позволяют оценить значения разности указанных корней. В подобных ситуациях приходится прибегать к исследованию функции, нахождению ее наибольшего и наименьшего значений, через которые и оценивать значения функции. Иногда удобно комбинировать различные способы получения оценок. Покажем решение характерного иррационального уравнения.
. Но эти способы оценки уже не позволяют оценить значения разности указанных корней. В подобных ситуациях приходится прибегать к исследованию функции, нахождению ее наибольшего и наименьшего значений, через которые и оценивать значения функции. Иногда удобно комбинировать различные способы получения оценок. Покажем решение характерного иррационального уравнения.
Завершая разговор о решении иррациональных уравнений функционально-графическим методом и методом оценки в частности, вспомним про одно обещание, данное в статье Решение иррациональных уравнений методом введения новой переменной. Там, мы решили иррациональное уравнение  довольно экзотическим способом через введение двух новых переменных, и обещали показать его решение более стандартным методом. Таким методом в данном случае выступает именно метод оценки. Так выполним обещанное.
довольно экзотическим способом через введение двух новых переменных, и обещали показать его решение более стандартным методом. Таким методом в данном случае выступает именно метод оценки. Так выполним обещанное.
Мы разобрались, как и когда применяется метод оценки для решения иррациональных уравнений, а также рассмотрели решения характерных примеров. Продолжим изучать методы решения иррациональных уравнений, для чего обратимся к материалу решение иррациональных уравнений через ОДЗ.
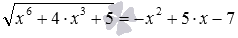
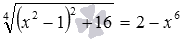 методом оценки.
методом оценки.




