Особенности введения новой переменной при решении иррациональных уравнений
Продолжаем изучение методов решения иррациональных уравнений. В этой статье мы рассмотрим метод введения новой переменной, а точнее, его использование при решении именно иррациональных уравнений. Основное внимание сосредоточим на особенностях введения новой переменной.
Вспомним алгоритм метода
Для начала приведем ссылку на подробное описание метода введения новой переменной. Рекомендуем освежить эту информацию в памяти. Для удобства давайте расположим перед глазами алгоритм решения уравнений методом введения новой переменной:
- Вводится новая переменная. Пусть это будет переменная t, которая вводится как g(x)=t, где g(x) – некоторое выражение, в результате чего исходное уравнение со старой переменной x преобразуется в уравнение с новой переменной t.
-
Решается полученное уравнение с новой переменной. При этом
- если уравнение не имеет корней, то делается вывод об отсутствии корней у исходного уравнения,
- если уравнение имеет корни, то выполняются следующие шаги алгоритма.
-
Осуществляется возврат к старой переменной. Для этого
- если решенное на предыдущем шаге уравнение имеет единственный корень, обозначим его t1, то составляется уравнение g(x)=t1,
-
если решенное на предыдущем шаге уравнение имеет два, три или любое другое, но конечное число корней, обозначим их t1, t2, …, tn, то составляется совокупность уравнений вида
 ,
,
-
если же решенное на предыдущем шаге уравнение имеет бесконечно много корней, и они составляют числовое множество T, то составляется совокупность уравнений, неравенств и двойных неравенств, отвечающая выражению g(x)∈T (например, если решением уравнения с новой переменной t является числовое множество (−∞, t1)∪{t2}∪[t3, t4), что то же самое
 , то соответствующая совокупность будет иметь вид
, то соответствующая совокупность будет иметь вид  ).
).
- Наконец, решается составленное уравнение или совокупность – ее решение дает искомое решение исходного уравнения.
В рамках текущей статьи основной интерес представляет первый шаг – введение новой переменной. В следующем пункте мы на примерах рассмотрим типичные приемы, которые используются для введения новой переменной при решении иррациональных уравнений.
Особенности введения новой переменной на примерах
Будем придерживаться следующей последовательности изложения:
-
Начнем с решения примеров, в которых очевидно, как ввести новую переменную. Здесь мы поговорим об иррациональных уравнениях, имеющих вид p(g(x))=r или p1(g(x))=p2(g(x)), r – некоторое число, а p, p1, p2, g – некоторые функции, где напрашивается введение новой переменной g(x)=t. Для наглядности приведем иррациональное уравнение такого вида
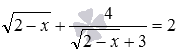 , где напрашивается замена
, где напрашивается замена  . Ниже мы решим его.
. Ниже мы решим его.
-
Дальше перейдем к случаям, когда выражение для замены почти очевидно, то есть, довольно просто просматривается, и небольшие преобразования уравнения позволяют выделить его явно (то есть, приводят уравнение к виду p(g(x))=0 или p1(g(x))=p2(g(x))). В качестве примера приведем иррациональное уравнение
 . Видите возможность замены
. Видите возможность замены  ? Она становится очевидна, после преобразования исходного уравнения к виду
? Она становится очевидна, после преобразования исходного уравнения к виду  .
.
-
Дальше перейдем к иррациональным уравнениям, в которых выражение, подходящее для замены его новой переменной, не очевидно, но его можно определить при помощи специальных приемов, учитывающих вид составных частей решаемого уравнения. После того, как подходящее выражение определено, осуществляется преобразование исходного уравнения с целью явно выделить выбранное выражение, что позволяет перейти к уравнению с новой переменной. Это касается, например, иррациональных уравнений, в записи которых подкоренные выражения одинаковые, но разные показатели корней. В частности, это касается уравнения
 .
.
-
После этого, затронем случаи, в которых возможность введения новой переменной можно лишь подозревать, и которая при удачном раскладе открывается только после довольно серьезных преобразований уравнения. Например, иррациональное уравнение
 лишь после ряда не самых очевидных преобразований приводится к виду
лишь после ряда не самых очевидных преобразований приводится к виду  , что открывает дорогу к замене
, что открывает дорогу к замене  .
.
- Наконец, упомянем про довольно экзотический способ решения иррациональных уравнений, подразумевающий введение не одной переменной, а нескольких переменных.
Итак, начнем с простейших случаев введения новой переменной при решении иррациональных уравнений.
Решим иррациональное уравнение 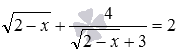 , которое мы уже приводили в пример чуть выше. Очевидно, что в данном случае возможна замена
, которое мы уже приводили в пример чуть выше. Очевидно, что в данном случае возможна замена  . Она нас приведет к рациональному уравнению, которое, как выяснится, имеет два корня, что при обратной замене даст совокупность двух простейших иррациональных уравнений, решение которой не представляет трудности. Для сравнения покажем альтернативный способ решения путем проведения преобразований, которые приведут к простейшему иррациональному уравнению.
. Она нас приведет к рациональному уравнению, которое, как выяснится, имеет два корня, что при обратной замене даст совокупность двух простейших иррациональных уравнений, решение которой не представляет трудности. Для сравнения покажем альтернативный способ решения путем проведения преобразований, которые приведут к простейшему иррациональному уравнению.
В следующем иррациональном уравнении также очевидна возможность введения новой переменной. Но оно примечательно тем, что при его решении нам не придется возвращаться к исходной переменной. Дело в том, что полученное после введения переменной уравнение не имеет решений, что означает отсутствие решений у исходного уравнения.
Иррациональное уравнение 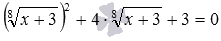 , как и предыдущее, удобно решать методом введения новой переменной. Более того, оно, как и предыдущее, не имеет решений. Но отсутствие корней определяется иными средствами: здесь уравнение, полученное после введения переменной
, как и предыдущее, удобно решать методом введения новой переменной. Более того, оно, как и предыдущее, не имеет решений. Но отсутствие корней определяется иными средствами: здесь уравнение, полученное после введения переменной  , решения имеет, а совокупность уравнений, записанная при проведении обратной замены, решений не имеет, поэтому не имеет решений и исходное уравнение. Разберем решение указанного уравнения.
, решения имеет, а совокупность уравнений, записанная при проведении обратной замены, решений не имеет, поэтому не имеет решений и исходное уравнение. Разберем решение указанного уравнения.
Завершим серию примеров, в которых замена очевидна, сложным с виду иррациональным уравнением 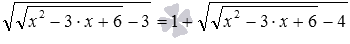 , содержащим в записи корень под корнем. Введение новой переменной часто делает структуру уравнения более понятной, что справедливо, в частности, для данного примера. Действительно, если принять
, содержащим в записи корень под корнем. Введение новой переменной часто делает структуру уравнения более понятной, что справедливо, в частности, для данного примера. Действительно, если принять  , то исходное иррациональное уравнение преобразуется в более простое иррациональное уравнение
, то исходное иррациональное уравнение преобразуется в более простое иррациональное уравнение  , которое можно решать, например, методом возведения обеих частей уравнения в квадрат. Приведем решение методом введения новой переменной, а также для сравнения покажем решение методом возведения обеих частей уравнения в квадрат.
, которое можно решать, например, методом возведения обеих частей уравнения в квадрат. Приведем решение методом введения новой переменной, а также для сравнения покажем решение методом возведения обеих частей уравнения в квадрат.
Записи всех предыдущих примеров содержали по несколько одинаковых выражений, которые мы и принимали за новую переменную. Все было просто и очевидно: видим подходящие одинаковые выражения и вместо них вводим новую переменную, что дает более простое уравнение с новой переменной. Сейчас мы продвинемся чуть дальше – будем разбираться, как решать иррациональные уравнения, в которых подходящее для замены выражение не столь очевидно, но довольно легко просматривается и выделяется в явном виде при помощи несложных преобразований.
Рассмотрим основные приемы, позволяющие явно выделить удобное для введения новой переменной выражение. Первый из них – это вынесение за скобки общего множителя. Проиллюстрируем сказанное.
Очевидно, в иррациональном уравнении  для того, чтобы ввести новую переменную, достаточно принять x2+x=t. А видна ли возможность также ввести новую переменную в уравнении
для того, чтобы ввести новую переменную, достаточно принять x2+x=t. А видна ли возможность также ввести новую переменную в уравнении 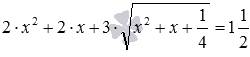 ? Такая возможность просматривается, ведь очевидно, что
? Такая возможность просматривается, ведь очевидно, что  . Последнее равенство позволяет провести равносильное преобразование уравнения, заключающееся в замене выражения тождественно равным ему выражением, не изменяющим ОДЗ, что дает возможность от исходного уравнения перейти к равносильному уравнению
. Последнее равенство позволяет провести равносильное преобразование уравнения, заключающееся в замене выражения тождественно равным ему выражением, не изменяющим ОДЗ, что дает возможность от исходного уравнения перейти к равносильному уравнению  и решать уже его. Покажем полное решение иррационального уравнения
и решать уже его. Покажем полное решение иррационального уравнения 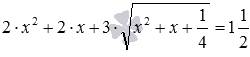 методом введения новой переменной.
методом введения новой переменной.
Что еще, помимо вынесения за скобки общего множителя, позволяет в иррациональном уравнении явно выделить удобное для введения новой переменной выражение? В определенных случаях – это определение корня, свойства корней и свойства степеней. Разберем характерные примеры.
Как бы мы ввели новую переменную при решении иррационального уравнения  ? Конечно, мы бы приняли
? Конечно, мы бы приняли  . А если бы стояла задача решить иррациональное уравнение
. А если бы стояла задача решить иррациональное уравнение 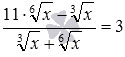 , видна ли возможность введения новой переменной как
, видна ли возможность введения новой переменной как  ? Явно – не видна, но такая возможность просматривается, так как на ОДЗ переменной x для этого уравнения в силу определения корня и свойств корней справедливо равенство
? Явно – не видна, но такая возможность просматривается, так как на ОДЗ переменной x для этого уравнения в силу определения корня и свойств корней справедливо равенство  , которое позволяет перейти к равносильному уравнению
, которое позволяет перейти к равносильному уравнению  .
.
Позволим себе небольшое обобщение на основе предыдущего примера. В случаях, когда показатель одного корня кратен показателю другого (k·n и k), обычно прибегают к равенству  и вводят новую переменную как
и вводят новую переменную как  . Так мы и действовали, решая уравнение
. Так мы и действовали, решая уравнение 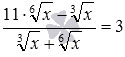 . Чуть дальше мы поговорим о том, как решать иррациональные уравнения с неравными и некратными показателями корней.
. Чуть дальше мы поговорим о том, как решать иррациональные уравнения с неравными и некратными показателями корней.
Стоит вкратце остановиться на введении новой переменной в иррациональных уравнениях, в которых содержится корень, а также подкоренное выражение и/или его некоторая степень. В этих случаях очевидно, что в качестве новой переменной следует принять корень. Например, при решении уравнения  мы бы приняли
мы бы приняли  , по определению корня преобразовали бы исходное уравнение к виду
, по определению корня преобразовали бы исходное уравнение к виду  , и после введения новой переменной пришли бы к квадратному уравнению 2·t2+3·t−2=0.
, и после введения новой переменной пришли бы к квадратному уравнению 2·t2+3·t−2=0.
В случаях чуть посложнее может потребоваться еще одно дополнительное преобразование уравнения для выделения выражения, совпадающего с подкоренным. Поясним это. Как бы мы ввели новую переменную в уравнении  ? Очевидно, выражение x2+5 совпадает с подкоренным выражением, поэтому, согласно информации предыдущего абзаца мы бы на базе определения корня перешли к равносильному уравнению
? Очевидно, выражение x2+5 совпадает с подкоренным выражением, поэтому, согласно информации предыдущего абзаца мы бы на базе определения корня перешли к равносильному уравнению  и ввели бы новую переменную как
и ввели бы новую переменную как  . А как бы мы вводили новую переменную, если бы имели дело не с уравнением
. А как бы мы вводили новую переменную, если бы имели дело не с уравнением  , а с уравнением
, а с уравнением  ? Да также. Просто сначала нам бы пришлось x2+1 представить как x2+5−4, чтобы явно выделить подкоренное выражение x2+5. То есть, мы бы от иррационального уравнения
? Да также. Просто сначала нам бы пришлось x2+1 представить как x2+5−4, чтобы явно выделить подкоренное выражение x2+5. То есть, мы бы от иррационального уравнения  перешли к равносильному уравнению
перешли к равносильному уравнению  , затем к уравнению
, затем к уравнению  , после чего с легкостью ввели бы новую переменную
, после чего с легкостью ввели бы новую переменную  .
.
В подобных случаях имеет место и другой более универсальный подход к введению новой переменной: в качестве новой переменной брать корень и на базе этого равенства остальные старые переменный выражать через новую. Для уравнения  мы бы приняли
мы бы приняли  , из этого равенства выразили бы x2 через t как t2−5 (
, из этого равенства выразили бы x2 через t как t2−5 ( ,
,  , x2+5=t2, x2=t2−5), откуда x2+1=t2−4. Это позволяет перейти к уравнению с новой переменной t2−4+3·t=0. Для отработки навыков решим типовое иррациональное уравнение.
, x2+5=t2, x2=t2−5), откуда x2+1=t2−4. Это позволяет перейти к уравнению с новой переменной t2−4+3·t=0. Для отработки навыков решим типовое иррациональное уравнение.
Введение новой переменной в подобных примерах может приводить к возникновению под знаками корней выражений, представляющих собой полные квадраты. Например, если в иррациональном уравнении  принять
принять  , то это приведет к уравнению
, то это приведет к уравнению  , где первое подкоренное выражение – это квадрат линейного двучлена t−2, а второе подкоренное выражение – квадрат линейного двучлена t−3. А от таких уравнений лучше всего переходить к уравнениям с модулями:
, где первое подкоренное выражение – это квадрат линейного двучлена t−2, а второе подкоренное выражение – квадрат линейного двучлена t−3. А от таких уравнений лучше всего переходить к уравнениям с модулями:  ,
,  ,
,  . Это связано с тем, что такие уравнения могут иметь бесконечное множество корней, при этом их решение путем возведением обеих частей уравнения в квадрат не позволит провести проверку подстановкой, а решение по определению корня приведет к необходимости решения иррационального неравенства. Решение такого примера мы покажем ниже в пункте переход от иррационального уравнения к уравнению с модулем.
. Это связано с тем, что такие уравнения могут иметь бесконечное множество корней, при этом их решение путем возведением обеих частей уравнения в квадрат не позволит провести проверку подстановкой, а решение по определению корня приведет к необходимости решения иррационального неравенства. Решение такого примера мы покажем ниже в пункте переход от иррационального уравнения к уравнению с модулем.
Когда еще довольно легко просматривается возможность введения новой переменной? Когда в записи уравнения фигурируют «перевернутые» дроби  и
и  (с Вашего позволения будем называть их взаимно обратными по аналогии со взаимно обратными числами). Как бы мы решали рациональное уравнение с такими дробями? Мы бы одну из таких дробей приняли за новую переменную t, при этом другая дробь выразилась бы через новую переменную как 1/t. В иррациональных же уравнениях так вводить новую переменную не совсем практично, так как для дальнейшего избавления от корней, скорее всего, придется вводить еще одну переменную. Лучше сразу принимать в качестве новой переменной корень из дроби. Ну а дальше преобразовать исходное уравнение при помощи одного из равенств
(с Вашего позволения будем называть их взаимно обратными по аналогии со взаимно обратными числами). Как бы мы решали рациональное уравнение с такими дробями? Мы бы одну из таких дробей приняли за новую переменную t, при этом другая дробь выразилась бы через новую переменную как 1/t. В иррациональных же уравнениях так вводить новую переменную не совсем практично, так как для дальнейшего избавления от корней, скорее всего, придется вводить еще одну переменную. Лучше сразу принимать в качестве новой переменной корень из дроби. Ну а дальше преобразовать исходное уравнение при помощи одного из равенств  и
и  , что позволит перейти к уравнению с новой переменной. Рассмотрим пример.
, что позволит перейти к уравнению с новой переменной. Рассмотрим пример.
Не стоит забывать про уже известные варианты замен. Например, в записи иррационального уравнения могут фигурировать выражения x+1/x и x2+1/x2, что заставляет задуматься о возможности введения новой переменной x+1/x=t. Эта мысль возникает не случайно, ведь мы так уже делали, когда решали возвратные уравнения. Такой способ введения новой переменной, как и другие уже известные нам способы, следует иметь в виду при решении иррациональных уравнений, как впрочем, и уравнений других видов.
Переходим к более сложным иррациональным уравнениям, в которых подходящее для введения новой переменной выражение разглядеть сложнее. И начнем с уравнений, в которых подкоренные выражения одинаковы, но, в отличие от разобранного выше случая, больший показатель одного корня не делится нацело на меньший показатель другого корня. Давайте разберемся, как правильно выбрать выражение, подходящее для введения новой переменной в таких случаях.
Когда подкоренные выражения одинаковые, а больший показатель одного корня k1 не делится нацело на меньший показатель другого корня k2, в качестве новой переменной можно принять корень степени НОК(k1, k2), где НОК – наименьшее общее кратное. Например, в иррациональном уравнении 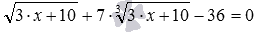 показатели корней равны 2 и 3, три не кратно двум, НОК(3, 2)=6, поэтому новую переменную можно ввести как
показатели корней равны 2 и 3, три не кратно двум, НОК(3, 2)=6, поэтому новую переменную можно ввести как  . Дальше определение корня, а также свойства корней позволяют преобразовать исходное уравнение, чтобы явно выделить выражение
. Дальше определение корня, а также свойства корней позволяют преобразовать исходное уравнение, чтобы явно выделить выражение  и дальше заменить его новой переменной. Приведем полное и подробное решение этого уравнения.
и дальше заменить его новой переменной. Приведем полное и подробное решение этого уравнения.
По аналогичным принципам вводится новая переменная в случаях, когда выражения под корнями отличаются степенями. Например, если в иррациональном уравнении переменная содержится только под корнями, а сами корни имеют вид  и
и  , то следует вычислить наименьшее общее кратное показателей корней НОК(3, 4)=12 и принять
, то следует вычислить наименьшее общее кратное показателей корней НОК(3, 4)=12 и принять  . При этом по свойствам корней и степеней корни
. При этом по свойствам корней и степеней корни  и
и  следует преобразовать как
следует преобразовать как  и
и  соответственно, что позволит ввести новую переменную.
соответственно, что позволит ввести новую переменную.
Похожим образом можно действовать и в иррациональных уравнениях, в которых под корнями с разными показателями находятся взаимно обратные дроби  и
и  . То есть, в качестве новой переменной целесообразно принимать корень с показателем, равным НОК показателей корней. Ну а дальше переходить к уравнению с новой переменной, что позволяют сделать равенства
. То есть, в качестве новой переменной целесообразно принимать корень с показателем, равным НОК показателей корней. Ну а дальше переходить к уравнению с новой переменной, что позволяют сделать равенства  и
и  , определение корня, а также свойства корней и степеней. Рассмотрим пример.
, определение корня, а также свойства корней и степеней. Рассмотрим пример.
Теперь поговорим об уравнениях, в которых возможность введения новой переменной можно лишь подозревать, и которая при удачном раскладе открывается только после довольно серьезных преобразований. Например, иррациональное уравнение 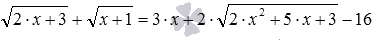 лишь после ряда не самых очевидных преобразований приводится к виду
лишь после ряда не самых очевидных преобразований приводится к виду  , что открывает дорогу к замене
, что открывает дорогу к замене  . Приведем решение этого примера.
. Приведем решение этого примера.
Напоследок внесем немного экзотики. Иногда иррациональное уравнение можно решить путем введения не одной, а нескольких переменных. Такой подход к решению уравнений предложен в учебнике [1, с. 241-242]. Там для решения иррационального уравнения  предлагается ввести две переменные
предлагается ввести две переменные  . В учебнике приведено краткое решение, давайте восстановим и детали.
. В учебнике приведено краткое решение, давайте восстановим и детали.
Мы разобрались с методом введения новой переменной при решении иррациональных уравнений. Можно двигаться дальше. Переходим к изучению метода разложения на множители при решении иррациональных уравнений.
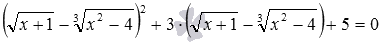

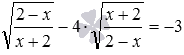 .
.

