Дифференциальные уравнения, примеры, решения

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.


В этой статье поговорим о решении линейных однородных и неоднородных дифференциальных уравнений порядка выше второго с постоянными коэффициентами. Такие уравнения имеют вид формула и формула, где формула - действительные числа, а функция f(x) непрерывна на интервале интегрирования X.

Сразу скажем, что аналитически решить такие уравнения далеко не всегда возможно и обычно используют приближенные методы. Однако в некоторых случаях возможно отыскать общее решение.


Сформулируем две теоремы, которые показывают, в каком виде искать общие решения ЛОДУ и ЛНДУ n-ого порядка.

Теорема.

Общим решением y0 линейного однородного дифференциального уравнения формула на интервале X с непрерывными коэффициентами формула на X является линейная комбинация n линейно независимых частных решений ЛОДУ формула с произвольными постоянными коэффициентами формула, то есть формула.

Теорема.

Общее решение y линейного неоднородного дифференциального уравнения формула на интервале X с непрерывными на том же промежутке X коэффициентами формула и функцией f(x) представляет собой сумму формула, где y0 - общее решение соответствующего ЛОДУ формула, а формула - какое-нибудь частное решение исходного ЛНДУ.

Таким образом, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами формула ищем в виде формула, где формула - какое-нибудь его частное решение, а формула – общее решение соответствующего однородного дифференциального уравнения формула.


Сначала разберемся как находить формула - общее решение ЛОДУ n-ого порядка с постоянными коэффициентами, а в конце статьи покажем как определить частное решение формула линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.

Алгебраическое уравнение n-ого порядка формула называется характеристическим уравнением линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами вида формула. Если мы найдем все n корней характеристического уравнения формула, то, исходя из их значений, можно определить n частных линейно независимых решений формула исходного ЛОДУ.

Перечислим все возможные варианты и разберем примеры на каждый из них.

  1. Если все решения формула характеристического уравнения формула действительные и различные, то линейно независимые частные решения имеют вид
    формула
    а общее решение ЛОДУ n-ого порядка с постоянными коэффициентами записывается как
    формула

    Пример.

    Найдите общее решение линейного однородного дифференциального уравнения третьего порядка с постоянными коэффициентами формула.

    Решение.

    Запишем характеристическое уравнение и найдем его корни, предварительно разложив многочлен в левой части равенства на множители способом группировки:
    формула

    Все три корня характеристического уравнения действительные и различные, поэтому общее решение ЛОДУ третьего порядка с постоянными коэффициентами имеет вид
    формула.

  2. Если все решения характеристического уравнения действительные и одинаковые, то есть, формула, то линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеют вид
    формула
    а общее решение ЛОДУ имеет вид
    формула

    Пример.

    Найдите общее решение дифференциального уравнения формула.

    Решение.

    Характеристическое уравнение этого ЛОДУ четвертого порядка имеет вид формула.

    Если обратиться к формуле бинома Ньютона, то характеристическое уравнение можно переписать в виде формула, откуда виден его четырехкратный корень k0 = 2.

    Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами есть
    формула.

  3. Если решениями характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами являются различные комплексно сопряженные пары формула, n=2m, то линейно независимые частные решения такого ЛОДУ имеют вид
    формула
    а общее решение записывается как
    формула

    Пример.

    Проинтегрируйте линейное однородное дифференциальное уравнение четвертого порядка с постоянными коэффициентами формула.

    Решение.

    Характеристическим уравнением данного ЛОДУ является формула. После проведения несложных преобразований и группировки получаем
    формула

    Отсюда легко найти две пары комплексно сопряженных корней характеристического уравнения формула и формула. Следовательно, общее решение исходного линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеет вид
    формула

  4. Если решениями характеристического уравнения являются совпадающие комплексно сопряженные пары формула, то линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеют вид
    формула
    а общее решение такого ЛОДУ есть
    формула

    Пример.

    Найдите общее решение ЛОДУ с постоянными коэффициентами формула.

    Решение.

    Запишем характеристическое уравнение данного линейного однородного дифференциального уравнения с постоянными коэффициентами и найдем его корни:
    формула

    То есть, решением характеристического уравнения является двукратная комплексно сопряженная пара формула. Поэтому общим решеним исходного линейного однородного дифференциального уравнения с постоянными коэффициентами является
    формула.

  5. Возможны любые комбинации предыдущих случаев, то есть, часть корней характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами действительные и различные, часть действительные и совпадающие, часть различных комплексно сопряженных пар и часть совпадающих комплексно сопряженных пар.

    Пример.

    Найдите общее решение дифференциального уравнения формула.

    Решение.

    Характеристическое уравнение данного линейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид формула.

    Многочлен в левой части равенства можно разложить на множители (смотрите раздел разложение многочлена на множители). Среди делителей свободного члена находим двукратный корень k1=k2=2 и корень k3=-3. Используя схему Горнера, приходим к разложению формула.

    Из квадратного уравнения формула находим оставшиеся корни формула.

    Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид
    формула

Итак, мы разобрали основные случаи, при которых можно найти y0 - общее решение ЛОДУ n-ого порядка с постоянными коэффициентами.

Теперь переходим к нахождению общего решения линейных неоднородных дифференциальных уравнений n-ого порядка с постоянными коэффициентами вида формула.

Их общее решение представляется в виде суммы общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ, то есть, как формула. Так как мы научились находить y0, то осталось научиться определять формула - частное решение линейного неоднородного дифференциального уравнения порядка n с постоянными коэффициентами.

Перечислим методы нахождения формула в зависимости от вида функции f(x), которая находится в правой части рассматриваемого ЛНДУ.

  1. Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде 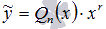формула, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю.
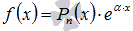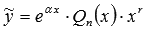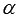  2. Если функция f(x) представлена произведением многочлена степени n и экспоненты формула, то частное решение ЛНДУ второго порядка ищется в виде формула, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных формула.
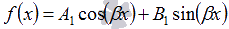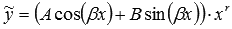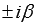  3. Если функция f(x) имеет вид формула, где А1 и В1 – числа, то частное решение ЛНДУ представляется как формула, где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных формула.
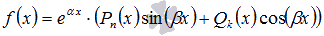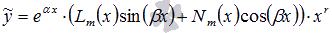  4. Если формула, то формула, где r – число комплексно сопряженных пар корней характеристического уравнения, равных 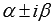формула, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m=max(n,k).

Все неизвестные коэффициенты находятся из равенства формула.

Для каждого из этих случаев подробные решения примеров можете посмотреть в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, так как принципы решения ЛНДУ степени выше второй абсолютно совпадают.

Для любого другого вида функции f(x) общее решение ЛНДУ можно найти методом вариации произвольных постоянных. Вот на методе вариации произвольных постоянных остановимся подробнее.

Если нам известны формула - n линейно независимых частных решений соответствующего ЛОДУ, то, варьируя произвольные постоянные, общее решение ЛНДУ n-ого порядка с постоянными коэффициентами можно записать как формула. Производные функций формула находятся из системы уравнений
формула
а сами функции формула определяются при последующем интегрировании.

Рассмотрим на примере.

Пример.

Найдите общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами формула.

Решение.

Характеристическое уравнение соответствующего ЛОДУ имеет вид формула. Корнями этого уравнения являются k1=0, k2=2 и k3=3. Следовательно, общее решение ЛОДУ имеет вид формула и частные линейно независимые решения есть формула.

Варьируем произвольные постоянные: формула.

Для нахождения C1(x), C2(x) и C3(x) составляем систему уравнений
формула

Решаем ее методом Крамера:
формула

Интегрируя формула с помощью таблицы первообразных, а формула и формула методом интегрирования по частям, получаем:

формула

Таким образом, искомое общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид

формула
где C4, C5 и C6 – произвольные постоянные.

Список литературы.

  • Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление.

Некогда разбираться?

Закажите решение




К началу страницы