Свойства определенного интеграла.
В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу.
Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.
Прежде чем перейти к основным свойствам определенного интеграла, условимся, что a не превосходит b.
-
Для функции y = f(x), определенной при x = a, справедливо равенство
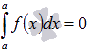 .
.
То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма
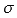 для любого разбиения промежутка [a; a] и любого выбора точек
для любого разбиения промежутка [a; a] и любого выбора точек 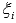 равна нулю, так как
равна нулю, так как 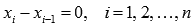 , следовательно, пределом интегральных сумм является ноль.
, следовательно, пределом интегральных сумм является ноль.
-
Для интегрируемой на отрезке [a; b] функции выполняется
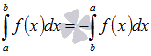 .
.
Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b.
-
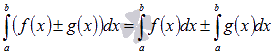 для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).
для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).
Доказательство.
Запишем интегральную сумму функции
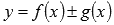 для данного разбиения отрезка и данного выбора точек
для данного разбиения отрезка и данного выбора точек 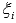 :
:
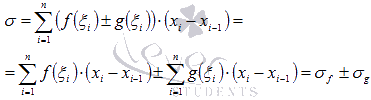
где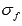 и
и 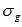 - интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.
- интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.
Переходя к пределу при
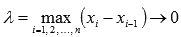 получим
получим 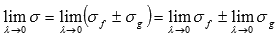 , что по определению интеграла Римана равносильно утверждению доказываемого свойства.
, что по определению интеграла Римана равносильно утверждению доказываемого свойства.
-
Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство
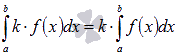 .
.
Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

-
Пусть функция y = f(x) интегрируема на интервале X, причем
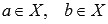 и
и 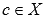 , тогда
, тогда 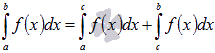 .
.
Это свойство справедливо как для
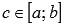 , так и для
, так и для 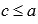 или
или 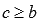 .
.
Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.
-
Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке
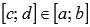 .
.
Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.
-
Если функция y = f(x) интегрируема на отрезке [a; b] и
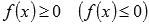 для любого значения аргумента
для любого значения аргумента 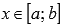 , то
, то 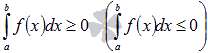 .
.
Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек
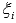 при
при 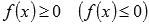 будет неотрицательной (не положительной).
будет неотрицательной (не положительной).
Следствие.
Для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x) справедливы неравенства:
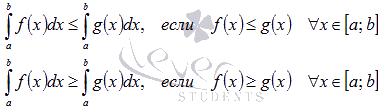
Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.
-
Пусть функция y = f(x) интегрируема на отрезке [a; b], тогда справедливо неравенство
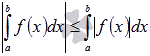 .
.
Доказательство.
Очевидно, что
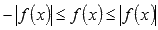 . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо
. В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо  . Это двойное неравенство можно записать как
. Это двойное неравенство можно записать как 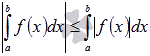 .
.
-
Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b] и
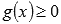 для любого значения аргумента
для любого значения аргумента 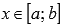 , тогда
, тогда 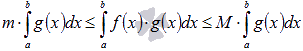 , где
, где 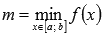 и
и 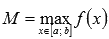 .
.
Доказательство проводится аналогично. Так как m и M – наименьшее и наибольшее значение функции y = f(x) на отрезке [a; b], то
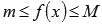 . Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству
. Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству 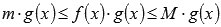 . Интегрируя его на отрезке [a; b], придем к доказываемому утверждению.
. Интегрируя его на отрезке [a; b], придем к доказываемому утверждению.
Следствие.
Если взять g(x) = 1, то неравенство примет вид
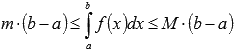 .
.
-
Первая формула среднего значения.
Пусть функция y = f(x) интегрируема на отрезке [a; b],
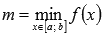 и
и 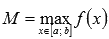 , тогда существует такое число
, тогда существует такое число 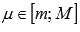 , что
, что 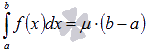 .
.
Следствие.
Если функция y = f(x) непрерывна на отрезке [a; b], то найдется такое число
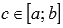 , что
, что 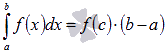 .
.
Первая формула среднего значения в обобщенной форме.
Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b],
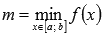 и
и 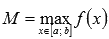 , а g(x) > 0 для любого значения аргумента
, а g(x) > 0 для любого значения аргумента 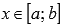 . Тогда существует такое число
. Тогда существует такое число 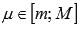 , что
, что 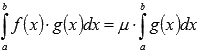 .
.
-
Вторая формула среднего значения.
Если на отрезке [a; b] функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число
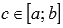 , что справедливо равенство
, что справедливо равенство 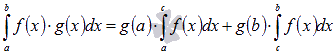 .
.
Некогда разбираться?