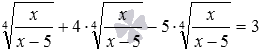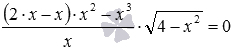Иррациональные уравнения, сводящиеся к числовым равенствам. Метод решения, примеры

Начнем с самого простого случая: с иррациональных уравнений, сводящихся к неверным числовым равенствам. Такие иррациональные уравнения не имеют решений. Дадим краткое обоснование этого факта.

Когда мы разбирали преобразования уравнений, то условились при решении уравнений прибегать лишь к преобразованиям, дающим либо равносильные уравнения, либо уравнения-следствия (как исключение мы допустили деление обеих частей уравнения на одно и то же выражение с переменной, при котором происходит сужение ОДЗ; это случай мы разобрали отдельно, здесь его опускаем). Так вот, допустим, осуществляя такие преобразования, мы пришли от исходного иррационального уравнения к неверному числовому равенству. Это означает, что последнее уравнение нашей цепочки преобразований не имеет решений, так как при подстановке в него любого значения переменной из ОДЗ мы будем получать неверное числовое равенство, соответствующее тому, к которому свелось исходное уравнение. А из отсутствия решений у последнего уравнения цепочки преобразований и из того, что оно является уравнением-следствием исходного уравнения, следует, что исходное иррациональное уравнение не имеет решений.

Теперь остановимся на случаях, когда иррациональные уравнения сводятся к верным числовым равенствам. Эту часть информации удобно рассмотреть с двух сторон:

• когда в цепочке преобразований нет возведения обеих частей уравнения в одну и ту же четную степень;
• и когда в цепочке преобразований есть возведение обеих частей уравнения в одну и ту же четную степень.

Если иррациональное уравнение приводится к верному числовому равенству без использования возведения обеих частей уравнения в одну и ту же четную степень, то его решением является множество, совпадающее с областью допустимых значений для исходного уравнения. Другими словами, любое число из ОДЗ для такого уравнения является решением этого уравнения. Обоснуем это.

Пусть цепочка переходов к равносильным уравнениям и уравнениям-следствиям получена без использования возведения обеих частей уравнения в одну и ту же четную степень, и она привела к верному числовому равенству. Это означает, что последнее уравнение этой цепочки имеет решением множество, совпадающее с его ОДЗ. Действительно, при подстановке в это уравнение любого значения из его ОДЗ, мы будем получать верное числовое равенство, соответствующее равенству, к которому свелось исходное уравнение. Мы знаем, что переход к уравнениям-следствиям может приводить к появлению посторонних корней, причем причин возможного возникновения посторонних корней две: из-за расширения ОДЗ и из-за возведения обеих частей уравнения в одну и ту же четную степень. Так как к последнему преобразованию мы не прибегали, то в нашем случае посторонние корни могли появиться лишь по причине расширения ОДЗ. А нам известно, что такие посторонние корни можно отсеять по ОДЗ для исходного уравнения. Из этого следует, что решением исходного иррационального уравнения является его ОДЗ.

Когда среди преобразований, приводящих иррациональное уравнение к верному числовому равенству, присутствует возведение обеих частей уравнения в четную степень, то нужно либо добавлять дополнительные условия, делающие это преобразование равносильным, либо отказываться от возведения обеих частей уравнения в одну и ту же степень в пользу другого метода решения. Почему же возведение в четную степень привносит такие сложности? Да потому, что это преобразование в общем случае неравносильное и может приводить к появлению посторонних корней, которые не всегда отсеиваются через ОДЗ.

Теперь разберем эти три представленных ситуации при решении характерных иррациональных уравнений.

К началу страницы

Откроем серию примеров решением иррационального уравнения, которое путем приведения подобных слагаемых сводится к неверному числовому равенству.

Следующее иррациональное уравнение сводится к верному числовому равенству, причем для этого не приходится прибегать к возведению обеих частей уравнения в одну и ту же четную степень. Решением этого уравнения является вся область допустимых значений.

Если вести преобразование следующего иррационального уравнения через уединение радикала с последующим возведением обеих частей уравнения в квадрат, то оно сведется к верному числовому равенству. Здесь нельзя спешить с выводом, что решением исходного уравнения является любое число из ОДЗ для него, так как в результате возведения обеих частей уравнения в одну и ту же степень могут появляться посторонние корни в пределах ОДЗ. В подобных случаях целесообразно поискать метод решения, позволяющий обойтись без возведения в одну и ту же степень.