Решение иррациональных уравнений через преобразования

Для начала дадим ссылку на подробное описание метода решения уравнений через преобразования. В этом пункте мы не будем дублировать эту информацию, но самые основные моменты перечислим.

Решение уравнений, в том числе и иррациональных, через преобразования состоит в использовании преобразований уравнения для выстраивании цепочки равносильных уравнений и уравнений-следствий с целью прийти к довольно простому уравнению, чтобы по его решению найти решение исходного уравнения.

Если все уравнения постороенной цепочки равносильные, то решение последнего уравнения является решением исходного уравнения.

Если в цепочке есть уравнения-следствия, то после решения последнего уравнения необходимо позаботиться об отсеивании корней, посторонних для исходного уравнения.

К началу страницы

Для решения иррациональных уравнений используются практически все преобразования уравнений, за исключением, разве что, логарифмирования и потенцирования. Давайте составим список преобразований, которые почти постоянно приходится применять при решении иррациональных уравнений:

• Замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями.
  • Перестановка местами слагаемых и множителей.
  • Раскрытие скобок.
  • Группировка слагаемых и/или множителей.
  • Вынесение за скобки общего множителя.
  • Замена числовых выражений их значениями.
  • Выполнение действий с одночленами и многочленами.
  • Приведение подобных слагаемых.
  • Сокращение дробей.
  • Замена нулем произведений с нулевыми множителями и дробей с нулем в числителе.
  • Использование тождеств, отражающих определения и свойства корней, степеней, логарифмов, тригонометрических функций и т.п.
• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа.
• Прибавление к обеим частям уравнения одного и того же выражения или вычитание из обеих частей уравнения одного и того же выражения.
• Перенос слагаемого из одной части уравнения в другую со знаком, измененным на противоположный.
• Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля.
• Умножение или деление обеих частей уравнения на одно и то же выражение.
• Возведение обеих частей уравнения в одну и ту же натуральную степень.
• Освобождение от внешней функции.

К началу страницы

Пришло время рассмотреть, как перечисленные в предыдущем пункте преобразования используются при решении иррациональных уравнений. Давайте остановимся на каждом преобразовании. Будем придерживаться последовательности изложения, которую диктует наш список. На очевидных преобразованиях сильно задерживаться не будем. А наиболее характерные для иррациональных уравнений преобразования рассмотрим подробно. Для них обговорим все нюансы, и посмотрим на них в готовых решениях характерных иррациональных уравнений.

Первое интересующее нас преобразование – это замена выражений в уравнении тождественно равными им выражениями. Оно является равносильным, если область допустимых значений для уравнения, полученного в результате преобразования, такая же, как ОДЗ для исходного уравнения. Из этого понятно, что есть две основные причины возникновения ошибок при проведении этого преобразования: первая – это изменение ОДЗ, происходящее в результате проведенного преобразования, вторая – это замена выражения не тождественно равным ему выражением. Разберем эти аспекты подробно и по порядку, рассматривая примеры типичных преобразований этого вида.

Сначала пробежимся по типичным преобразованиям уравнений, заключающимся в замене выражения тождественно равным ему выражением, которые всегда являются равносильными:

• Перестановка местами слагаемых и множителей. Это преобразование можно проводить как в левой, так и в правой части иррационального уравнения. Оно может использоваться, например, для группировки и последующего приведения подобных слагаемых с целью упрощения вида уравнения для его дальнейшего решения. Перестановка местами слагаемых или множителей, очевидно, является равносильным преобразованием уравнения. Оно и понятно: исходное выражение и выражение с переставленными местами слагаемыми или множителями являются тождественно равными (если, конечно, перестановка осуществлена корректно), и очевидно, что такое преобразование не изменяет ОДЗ. Приведем пример. В левой части иррационального уравнения в произведении x·3·x можно переставить местами первый и второй множители x и 3, что в дальнейшем позволит представить многочлен, находящийся под знаком корня, в стандартном виде. А в правой части уравнения в сумме 4+x+5 можно провести перестановку местами слагаемых 4 и x, что в дальнейшем позволит выполнить сложение чисел 4 и 5. После указанных перестановок иррациональное уравнение примет вид , полученное уравнение равносильно исходному.
• Раскрытие скобок. Равносильность этого преобразования уравнений очевидна: выражения до и после раскрытия скобок являются тождественно равными и имеют одинаковую область допустимых значений. Для примера возьмем иррациональное уравнение . Его решение требует раскрытия скобок. Раскрыв скобки в левой части уравнения, а также в правой части уравнения придем к равносильному уравнению .
• Группировка слагаемых и/или множителей. Это преобразование уравнения по своей сути представляет замену какого-либо выражения, являющегося частью уравнения, тождественно равным ему выражением со сгруппированными слагаемыми или множителями. Очевидно, при этом не изменяется ОДЗ. Значит, указанное преобразование уравнения является равносильным. Для иллюстрации возьмем иррациональное уравнение . Перестановка слагаемых (о ней мы говорили двумя абзацами выше) и группировка слагаемых позволяет перейти к равносильному уравнению . Цель подобной группировки слагаемых отчетливо просматривается - провести следующее равносильное преобразование , что позволит ввести новую переменную и решить иррациональное уравнение.
• Вынесение за скобки общего множителя. Понятно, что выражения до вынесения общего множителя за скобки и после вынесения за скобки общего множителя являются тождественно равными. Также понятно, что вынесение общего множителя за скобки не изменяет ОДЗ. Поэтому, вынесение за скобки общего множителя в выражении, находящемся в составе уравнения, является равносильным преобразованием уравнения. Такое преобразование используется, например, для представления левой части уравнения в виде произведения с целью его решения методом разложения на множители. Вот конкретный пример. Рассмотрим иррациональное уравнение . Левую часть этого уравнения можно представить в виде произведения, для этого нужно вынести за скобки общий множитель . В результате этого преобразования будет получено иррациональное уравнение , равносильное исходному, которое может быть решено методом разложения на множители.
• Замена числовых выражений их значениями. Понятно, что если в записи уравнения присутствует некоторое числовое выражение, и мы заменим это числовое выражение его значением (правильно вычисленным), то такая замена будет равносильной. Действительно, ведь по сути происходит замена выражения тождественно равным ему выражением и при этом не изменяется ОДЗ уравнения. Так, заменив в иррациональном уравнении сумму двух чисел −3 и 1 значением этой суммы, которое равно −2, получим равносильное иррациональное уравнение . Аналогично можно провести равносильное преобразование иррационального уравнения , выполнив действия с числами под знаком корня (1+2=3 и ), это преобразование приведет нас к равносильному иррациональному уравнению . А его решить несложно.
• Выполнение действий с одночленами и многочленами, находящимися в записи иррационального уравнения. Понятно, что правильное выполнение этих действий будет приводить к равносильному уравнению. Действительно, при этом будет происходить замена выражения тождественно равным ему выражением и не будет изменяться ОДЗ. К примеру, в иррациональном уравнении можно сложить одночлены x² и 3·x² и перейти к равносильному ему уравнению . Еще пример: вычитание многочленов в левой части иррационального уравнения является равносильным преобразованием, которое приводит к равносильному уравнению .

Продолжаем рассматривать преобразования уравнений, состоящие в замене выражений тождественно равными им выражениями. Такие преобразования могут быть и неравносильными, так как могут изменять ОДЗ. В частности, может происходить расширение ОДЗ. Это может иметь место при приведении подобных слагаемых, при сокращении дробей, при замене нулем произведения с несколькими нулевыми множителями или дроби с равным нулю числителем и наиболее часто при использовании формул, соответствующих свойствам корней. Кстати, небрежное использование свойств корней может приводить и к сужению ОДЗ. И если преобразования, расширяющие ОДЗ, допустимы при решении уравнений (они могут быть причиной возникновения посторонних корней, которые определенным образом отсеиваются), то от преобразований, сужающих ОДЗ, нужно в обязательном порядке отказаться, так как они могут быть причиной потери корней. Остановимся на этих моментах.

• Приведение подобных слагаемых в уравнении может быть неравносильным преобразованием! Приведение подобных слагаемых может дать нуль, при этом ОДЗ может расшириться. Вот пример. ОДЗ для иррационального уравнения определяется условиями , они задают множество [−1, 0)∪(0, +∞). Преобразование, заключающееся в приведении подобных слагаемых 1/x, приводит уравнение к виду , для него ОДЗ есть множество [−1, +∞). Очевидно, ОДЗ расширилась числом 0. Для данного примера это преобразование приводит к появлению постороннего корня 0, так как корнями уравнения являются числа 0 и −1, но 0 не является корнем исходного уравнения. Приведем еще один пример расширения ОДЗ при приведении подобных слагаемых в уравнении. Приведение подобных слагаемых в уравнении приводит к уравнению . Это преобразование расширяет ОДЗ (для исходного уравнения областью допустимых значений является множество всех неотрицательных чисел, а для полученного – множество всех действительных чисел), что может вызвать появление посторонних корней. Так что при таком ходе решения нужно будет обязательно позаботиться об отсеивании посторонних корней.
• Сокращение дробей в уравнении может способствовать расширению ОДЗ! Проиллюстрируем сказанное. Рассмотрим иррациональное уравнение . Сократив дробь в левой части уравнения, мы придем к уравнению . Посмотрим, что при этом происходит с ОДЗ. ОДЗ для исходного уравнения есть множество (−2, 1]∪[3, +∞), а для полученного – (−∞, 1]∪[3, +∞). Очевидно, ОДЗ расширилась. В нашем случае это проходит безболезненно – посторонние корни не появляются. Но в других случаях могут и появиться. Так что если преобразования уравнения были связаны с сокращением дробей, то не стоит забывать о проверке с целью отсеивания посторонних корней.
• Из-за замены нулем произведений с нулевыми множителями и дробей с нулем в числителе может расшириться ОДЗ! Вот пример. Рассмотрим иррациональное уравнение , для него ОДЗ определяется условиями , которые задают числовое множество [2, +∞). Замена произведения и дроби в правой части уравнения нулями дает уравнение . При этом происходит расширение ОДЗ до множества (−∞, −1]∪[2, +∞). В нашем случае такое преобразование уравнения оказывается неравносильным и влечет появление постороннего корня −1.
• Очень часто преобразования иррациональных уравнений, проводящиеся на базе определения корня, свойств корней и свойств степеней, бывают неравносильными! Таким образом, работая с корнями и степенями, нужно все время быть на чеку: смотреть, не изменяется ли ОДЗ при проведении преобразования, и правильно ли мы используем свойства корней (тождественным ли выражением мы заменяем выбранное выражение). Объять все многообразие таких преобразований практически невозможно, поэтому мы ограничимся решением двух, но очень характерных иррациональных уравнений.

Первое иррациональное уравнение таково 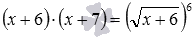. Его решение начинается с преобразования уравнения к виду на базе одного из свойств степеней. Это преобразование является равносильным, так как выражение заменяется тождественно равным выражением, и ОДЗ при этом не изменяется. А вот следующий переход к уравнению , проводящийся на базе определения корня, уже может быть неравносильным преобразованием уравнения, так как при таком преобразовании расширяется ОДЗ. Покажем полное решение этого уравнения.

Второе иррациональное уравнение, хорошо подходящее для иллюстрации того, что преобразования иррациональных уравнений с использованием свойств корней и определения корня могут быть неравносильными, имеет вид 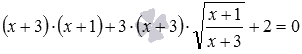. Хорошо, если Вы не позволите себе начинать решение так


или так


чтобы дальше воспользоваться методом введения новой переменной. Разберем, в чем здесь подвох.

Начинаем с первого случая. Первое преобразование - переход от исходного иррационального уравнения 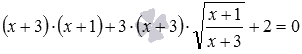к уравнению состоит в замене выражения x+3 выражением . Эти выражения тождественно равные. Но при такой замене происходит сужение ОДЗ с множества (−∞, −3)∪[−1, +∞) до множества [−1, +∞). А мы договорились отказаться от преобразований, сужающих ОДЗ, так как они могут приводить к потере корней.

А что не так во втором случае? Расширение ОДЗ при последнем переходе от к числом −3? Не только это. Большую озабоченность вызывает первый переход от исходного иррационального уравнения 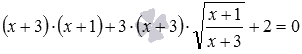к уравнению . Суть этого перехода – замена выражения x+3 выражением . Но эти выражения не являются тождественно равными: при x+3<0 значения этих выражений не совпадают. Действительно, согласно свойству квадратного корня из квадрата , откуда следует, что .

Так как же тогда решать это иррациональное уравнение 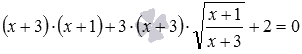? Здесь лучше всего сразу вводить новую переменную , при этом (x+3)·(x+1)=t². Приведем подробное решение.

Подведем итог по первому из разбираемых преобразований уравнений – замене выражения, находящегося в составе уравнения, тождественно равным ему выражением. Каждый раз при его проведении необходимо выполнение двух условий: первое - чтобы выражение заменялось именно тождественно равным выражением и второе - чтобы при этом не происходило сужение ОДЗ. Если при такой замене ОДЗ не изменяется, то в результате преобразования получится равносильное уравнение. Если при такой замене происходит расширение ОДЗ, то могут появиться посторонние корни, и необходимо позаботиться об их отсеивании.

Переходим ко второму преобразованию списка – прибавлению к обеим частям уравнения одного и того же числа и вычитанию из обеих частей уравнения одного и того же числа. Это равносильное преобразование уравнения. Обычно мы прибегаем к нему, когда в левой и правой части уравнения находятся одинаковые числа, вычитание из обеих частей уравнения этих чисел позволяет в дальнейшем избавиться от них. Например, и в левой и в правой части иррационального уравнения есть слагаемое 3. Вычитание тройки из обеих частей уравнения приводит к уравнению , которое после выполнения действий с числами принимает вид и дальше упрощается до . По результату рассматриваемое преобразование перекликается с переносом слагаемого из одной части уравнения в другую с противоположным знаком, но об этом преобразовании чуть позже. Есть и другие примеры применения этого преобразования при решении иррациональных уравнений. Например, в иррациональном уравнении прибавление к обеим частям числа 3 нужно для организации полного квадрата в левой части уравнения и дальнейшего преобразования уравнения к виду с целью введения новой переменной.

Обобщение только что рассмотренного преобразования – это прибавление к обеим частям уравнения или вычитание из обеих частей уравнения одного и того же выражения. Это преобразование уравнений является равносильным тогда, когда не изменяется ОДЗ. Данное преобразование проводится в основном для того, чтобы в дальнейшем избавиться от одинаковых слагаемых, находящихся одновременно и в левой и в правой части уравнения. Приведем пример. Допустим перед нами иррациональное уравнение . Очевидно, что и в левой и в правой части уравнения присутствует слагаемое . Резонно вычесть это выражение из обеих частей уравнения: . В нашем случае при таком переходе не изменяется ОДЗ, поэтому проделанное преобразование является равносильным. А делается оно для того, чтобы свести решение исходного уравнения к решению более простого иррационального уравнения .

Теперь посмотрим, как при решении иррациональных уравнений используется перенос слагаемых из одной части уравнения в другую с противоположным знаком. Это преобразование уравнения всегда равносильное. Сфера его применения довольно широка. С его помощью можно, например, уединить радикал или собрать подобные слагаемые в одной части уравнения, чтобы потом привести их и тем самым упростить вид уравнения. Приведем пример. Для решения иррационального уравнения можно перенести слагаемые −1 и в правую часть, изменив их знак, это даст равносильное уравнение , которое можно решать дальше, например, методом возведения обеих частей уравнения в квадрат.

Движемся дальше по пути рассмотрения преобразований уравнений к умножению или делению обеих частей уравнения на одно и то же число, отличное от нуля. Это преобразование является равносильным преобразованием уравнения. Умножение обеих частей уравнения на одно и то же число используется в основном для перехода от дробей к целым числам. Например, чтобы в иррациональном уравнении избавиться от дробей следует умножить обе его части на 8, что дает равносильное уравнение , которое дальше приводится к виду . Деление обеих частей уравнения проводится в основном с целью уменьшения числовых коэффициентов. Например, обе части иррационального уравнения целесообразно разделить на набольший общий делитель (НОД) числовых коэффициентов 18 и 12, то есть, на 6, такое деление дает равносильное уравнение , от которого в дальнейшем можно перейти к уравнению , имеющему меньшие, но тоже целые коэффициенты.

Следующее преобразование уравнения – это умножение и деление обеих частей уравнения на одно и то же выражение. Данное преобразование равносильное тогда, когда выражение, на которое производится умножение или деление, не изменяет область допустимых значений переменной и не обращается на ней в нуль. Обычно умножение обеих частей на одно и то же выражение по целям похоже на умножение обеих частей уравнения на одно и то же число. Наиболее часто к этому преобразованию прибегают, чтобы дальнейшими преобразованиями избавиться от дробей. Покажем это на примере решения иррационального уравнения.

Не обойдем стороной и иррациональные уравнения, для решения которых приходится прибегать к делению обеих частей уравнения на одно и то же выражение. Чуть выше мы отметили, что такое деление является равносильным преобразованием, если оно не влияет на ОДЗ и это выражение на ОДЗ не обращается в нуль. Но иногда деление приходится проводить и на выражение, обращающееся в нуль на ОДЗ. Так вполне можно поступать, если при этом отдельно проверять нули этого выражения на предмет того, нет ли среди них корней решаемого уравнения, иначе при таком делении эти корни могут потеряться.

Следующее преобразование иррациональных уравнений, которое мы затронем в этом пункте, заключается в возведении обеих частей уравнения в одну и ту же степень. Это преобразование можно назвать типичным для иррациональных уравнений, так как практически не используется при решении уравнений других видов. Это преобразование заслуживает детального и всестороннего изучения. Давайте вынесем этот вопрос в отдельную статью: решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень. Там дана необходимая теория и приведено множество примеров проведения этого преобразования при решении иррациональных уравнений. Здесь не будем повторяться, а лишь напомним, что в общем случае это преобразование не является равносильным. Оно может приводить к появлению посторонних корней. Поэтому, если в процессе решения мы обращались к этому преобразованию, то найденные корни нужно обязательно проверить на наличие среди них посторонних корней.

Про преобразование, заключающееся в освобождении от внешней функции, тоже поговорим отдельно. Вот соответствующий материал: Решение иррациональных уравнений методом освобождения от внешней функции.