Решение уравнений через ОДЗ
При решении уравнений мы обязаны находиться в рамках области допустимых значений (ОДЗ) переменной для этих уравнений. Решение уравнений определенных видов не требует явного нахождения ОДЗ. Например, мы обычно не говорим ни слова об области допустимых значений при решении линейных уравнений. Но это не из-за того, что мы ее не учитываем, а из-за того, что для любого линейного уравнения ОДЗ есть множество все действительных чисел, что очевидно, и мы в любом случае будем в ее рамках. В других случаях ОДЗ приходится находить отдельно, например, для преобразования уравнения или для отсеивания посторонних корней. А иногда ОДЗ оказывается чуть ли не самостоятельным инструментом решения уравнений. В этой статье мы как раз остановимся на этих ситуациях. То есть, здесь мы разберем, какие уравнения могут быть решены через ОДЗ, и как проводится их решение.
Какие уравнения можно решить через ОДЗ?
Через ОДЗ могут быть решены уравнения, ОДЗ для которых есть пустое множество или конечный набор чисел. То есть, индикатором того, может ли уравнение быть решено через ОДЗ, является сама область допустимых значений. Определить по внешнему виду уравнения, можно ли его решить через ОДЗ, нет возможности.
Например, ОДЗ для уравнения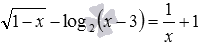 
есть пустое множество, и это уравнение может быть решено через ОДЗ. Другой пример: область допустимых значений переменной для уравнения 
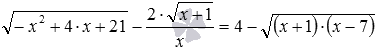состоит из двух чисел −1 и 7, это уравнение тоже может быть решено через ОДЗ. А вот уравнение 
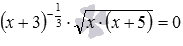не решить через ОДЗ, так как ОДЗ в этом случае представляет собой числовой промежуток [0, +∞), который не является ни пустым, ни конечным множеством.
Через ОДЗ решаются уравнения любых видов. Главное, чтобы ОДЗ удовлетворяла указанным выше условиям.
Как решать уравнение через ОДЗ?
Допустим, нам дано задание решить уравнение. Мы нашли ОДЗ для этого уравнения, и ею оказалось пустое множество. Что это означает? Это означает, что заданное уравнение не имеет смысла ни для какого значения переменной. Естественно, такое уравнение не имеет решений.
А теперь допустим, что ОДЗ представляет собой конечный набор чисел. Что нам это дает в плане поиска решения уравнения? Понятно, что мы можем проверить подстановкой каждое число из ОДЗ на предмет того, является ли оно корнем уравнения. Все числа из ОДЗ, которые будут удовлетворять заданному уравнению, являются решениями этого уравнения.
Алгоритм
Представим рассуждения из предыдущего пункта в виде алгоритма решения уравнений через ОДЗ:
-
Находим ОДЗ переменной для заданного уравнения.
- Если ОДЗ есть пустое множество, то делаем вывод об отсутствии решений.
- Если ОДЗ есть конечный набор чисел, то переходим ко второму пункту.
- Если ОДЗ представляет собой иное множество, то ищем другой метод решения.
- Осуществляем проверку подстановкой всех чисел из ОДЗ. Те из них, которые удовлетворяют решаемому уравнению, являются его решениями.
Решения характерных примеров
Рассмотрим решения двух характерных уравнени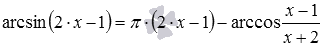й 
и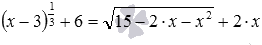 
. Первое из них подходит под случай, когда ОДЗ есть пустое множество, а второй – когда ОДЗ есть конечный набор чисел. Стоит заметить, что при решении уравнений через ОДЗ часто главную сложность представляет именно нахождение ОДЗ, остальные действия обычно значительно проще.
В следующем примере ОДЗ представляет собой единственное число. Через проверку подстановкой выясняется, что это число является корнем.
В заключение дадим ссылку на решение иррационального уравнения 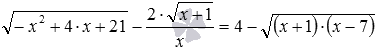, которое мы приводили в пример в первом пункте этой статьи. ОДЗ для него, в отличие от предыдущего примера, состоит из двух чисел, одно из которых является корнем уравнения, а другое – нет. Вот решение этого уравнения через ОДЗ.