Метод возведения обеих частей уравнения в одну и ту же степень
Продолжаем изучать методы решения уравнений. Сейчас мы в деталях разберем метод возведения обеих частей уравнения в одну и ту же степень. Начнем с теории: рассмотрим, для решения каких уравнений применяется метод, опишем, в чем он состоит, приведем теоретическое обоснование метода возведения обеих частей уравнения в одну и ту же степень, запишем соответствующие алгоритмы решения уравнений. После этого сосредоточимся на практике и рассмотрим разнообразные примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень.
Для решения каких уравнений применяется
Метод возведения обеих частей уравнения в одну и ту же степень в первую очередь применяется для решения иррациональных уравнений. Это объясняется тем, что возведение в натуральную и большую единицы степень позволяет избавляться от корней. Например, возведение в степень позволяет избавляться от корней при решении следующих уравнений:
-
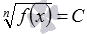 , C≥0, в частности,
, C≥0, в частности,  ,
,  и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению 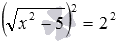 , и дальше – к сравнительно простому уравнению без знаков корней x2−5=4. Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x2−5=4. Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению 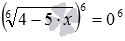 и дальше - к элементарному уравнению 4−5·x=0.
и дальше - к элементарному уравнению 4−5·x=0.
-
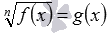 , например,
, например,  ,
,  и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
-
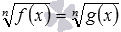 и
и  , таких как
, таких как 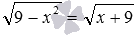 ,
, 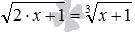 и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
-
уравнений с двумя, тремя корнями в записи, например,
 и
и  . В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
-
уравнений, в которых под знаком корня находятся другие корни, к примеру,
 . Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
- и это не весь список.
Метод возведения обеих частей уравнения в одну и ту же степень используется и для решения некоторых уравнений, в которых переменная находится в основаниях степеней с дробными показателями. Например, уравнение  можно решить методом возведения его обеих частей в дробную степень 6/11.
можно решить методом возведения его обеих частей в дробную степень 6/11.
Также метод возведения частей уравнения в степень применяется при решении некоторых степенных уравнений, в которых фигурируют иррациональные показатели. В пример приведем два уравнения  и
и  . Возведение их обеих частей в одну и ту же степень (в первом случае в степень
. Возведение их обеих частей в одну и ту же степень (в первом случае в степень  , во втором – в степень
, во втором – в степень  ) позволяет избавиться от степеней с иррациональными показателями и перейти к сравнительно простым уравнениям.
) позволяет избавиться от степеней с иррациональными показателями и перейти к сравнительно простым уравнениям.
В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
Метод состоит в переходе к уравнению, которое получается из исходного путем возведения его обеих частей в одну и ту же степень, и нахождении решения исходного уравнения по решению полученного уравнения.
На практике наиболее часто прибегают к возведению обеих частей уравнения в одну и ту же натуральную степень, большую единицы, то есть, в квадрат, куб и т.д. Делается это на базе следующего утверждения:
Утверждение
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень, большую единицы, дает равносильное уравнение (см. равносильные уравнения и уравнения-следствия).
Реже приходится обращаться к возведению обеих частей уравнения в другие степени, в частности, в дробные рациональные и иррациональные. В этих случаях отталкиваются от такого утверждения:
Утверждение
Уравнение A(x)=B(x), на области допустимых значений переменной x для которого A(x)>0 или A(x)≥0, B(x)>0 или B(x)≥0, равносильно уравнению Ar(x)=Br(x), где r – положительное действительное число.
Обоснование метода
Обоснованием метода возведения обеих частей уравнения в одну и ту же степень является доказательство утверждений из предыдущего пункта. Приведем эти доказательства.
Утверждение
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Доказательство
Докажем его для уравнений с одной переменной. Для уравнений с несколькими переменными принципы доказательства те же.
Пусть A(x)=B(x) – исходное уравнение и x0 – его корень. Так как x0 является корнем этого уравнения, то A(x0)=B(x0) – верное числовое равенство. Мы знаем такое свойство числовых равенств: почленное умножение верных числовых равенств дает верное числовое равенство. Умножим почленно 2·k, где k – натуральное число, верных числовых равенств A(x0)=B(x0), это нам даст верное числовое равенство A2·k(x0)=B2·k(x0). А полученное равенство означает, что x0 является корнем уравнения A2·k(x)=B2·k(x), которое получено из исходного уравнения путем возведения его обеих частей в одну и ту же четную натуральную степень 2·k.
Для обоснования возможности существования корня уравнения A2·k(x)=B2·k(x), который не является корнем исходного уравнения A(x)=B(x), достаточно привести пример. Рассмотрим иррациональное уравнение  , и уравнение
, и уравнение  , которое получено из исходного путем возведением его обеих частей в квадрат. Несложно проверить, что нуль является корнем уравнения
, которое получено из исходного путем возведением его обеих частей в квадрат. Несложно проверить, что нуль является корнем уравнения  , действительно,
, действительно,  , что то же самое 4=4 - верное равенство. Но при этом нуль является посторонним корнем для уравнения
, что то же самое 4=4 - верное равенство. Но при этом нуль является посторонним корнем для уравнения  , так как после подстановки нуля получаем равенство
, так как после подстановки нуля получаем равенство  , что то же самое 2=−2, которое неверное. Этим доказано, что уравнение, полученное из исходного путем возведения его обеих частей в одну и ту же четную степень, может иметь корни, посторонние для исходного уравнения.
, что то же самое 2=−2, которое неверное. Этим доказано, что уравнение, полученное из исходного путем возведения его обеих частей в одну и ту же четную степень, может иметь корни, посторонние для исходного уравнения.
Так доказано, что возведение обеих частей уравнения в одну и ту же четную натуральную степень приводит к уравнению-следствию.
Остается доказать, что возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Покажем, что каждый корень уравнения является корнем уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, и обратно, что каждый корень уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, является корнем исходного уравнения.
Пусть перед нами уравнение A(x)=B(x). Пусть x0 – его корень. Тогда является верным числовое равенство A(x0)=B(x0). Изучая свойства верных числовых равенств, мы узнали, что верные числовые равенства можно почленно умножать. Почленно умножив 2·k+1, где k – натуральное число, верных числовых равенств A(x0)=B(x0) получим верное числовое равенство A2·k+1(x0)=B2·k+1(x0), которое означает, что x0 является корнем уравнения A2·k+1(x)=B2·k+1(x). Теперь обратно. Пусть x0 – корень уравнения A2·k+1(x)=B2·k+1(x). Значит числовое равенство A2·k+1(x0)=B2·k+1(x0) - верное. В силу существования корня нечетной степени из любого действительного числа и его единственности будет верным и равенство  . Оно в свою очередь в силу тождества
. Оно в свою очередь в силу тождества  , где a – любое действительное число, которое следует из свойств корней и степеней, может быть переписано как A(x0)=B(x0). А это означает, что x0 является корнем уравнения A(x)=B(x).
, где a – любое действительное число, которое следует из свойств корней и степеней, может быть переписано как A(x0)=B(x0). А это означает, что x0 является корнем уравнения A(x)=B(x).
Так доказано, что возведение обеих частей иррационального уравнения в нечетную степень дает равносильное уравнение.
Доказанное утверждение пополняет известный нам арсенал, использующийся для решения уравнений, еще одним преобразованием уравнений – возведением обеих частей уравнения в одну и ту же натуральную степень. Возведение в одну и ту же четную степень обеих частей уравнения является преобразованием, приводящим к уравнению-следствию, а возведение в нечетную степень – равносильным преобразованием. На этом преобразовании базируется метод возведения обеих частей уравнения в одну и ту же степень.
Утверждение, касающееся возведения обеих частей уравнения в одну и ту же положительную действительную степень, доказывается аналогично с опорой на единственность степени положительного числа с действительным показателем.
Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
Есть смысл записать три алгоритма решения уравнений методом возведения обеих частей уравнения в одну и ту же степень: первый – для возведения в нечетную степень, второй – для возведения в четную степень, третий – для возведения в ненатуральную положительную степень.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же нечетную степень:
- Обе части уравнения возводятся в одну и ту же нечетную степень 2·k+1.
- Решается полученное уравнение. Его решение есть решение исходного уравнения.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же четную степень:
- Обе части уравнения возводятся в одну и ту же четную степень 2·k.
- Решается полученное уравнение.
- Если полученное уравнение не имеет корней, то делается вывод об отсутствии корней у исходного уравнения.
- Если полученное уравнение имеет корни, то проводится отсеивание посторонних корней любым методом, не завязанным на области допустимых значений, например, через проверку подстановкой.
Обратите внимание: этот алгоритм, в отличие от предыдущего, содержит пункт, касающийся отсеивания посторонних корней. Это связано с тем, что возведение обеих частей уравнения в одну и ту же нечетную степень приводит к равносильному уравнению, а возведение обеих частей уравнения в четную степень в общем случае приводит к уравнению-следствию. Поэтому, в результате возведения в нечетную степень посторонние корни не возникают, а при возведении в четную степень посторонние корни могут появиться. Таким образом, при возведении частей уравнения в четную степень возникает необходимость в отсеивании посторонних корней. Почему отсеивание посторонних корней в этом случае нужно проводить методом, не использующим ОДЗ? Потому что возведение обеих частей уравнения в четную степень может приводить к появлению посторонних корней в пределах ОДЗ, и отсеять их по ОДЗ или по условиям ОДЗ невозможно.
Наконец, запишем алгоритм решения уравнений методом возведения обеих частей в одну и ту же положительную дробную рациональную или иррациональную степень:
- Убеждаемся, что выражения в левой и правой части уравнения не принимают отрицательных значений на ОДЗ для решаемого уравнения.
- Возводим обе части уравнения в одну и ту же положительную степень.
- Решаем полученное уравнение. Его решение дает искомое решение исходного уравнения.
Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
Большое количество попадающих под разбираемую тему примеров с подробными решениями приведено в статье решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. В добавление к этим примерам стоит разобрать решение уравнения через возведение обеих частей уравнения в одну и ту же степень, не являющуюся натуральным числом.
Пример
Решите уравнение 
Решение
Решать заданное уравнение можно несколькими разными методами. Например, можно провести решение методом логарифмирования. Также можно преобразовать уравнение к виду  и перейти к уравнению
и перейти к уравнению  на основании метода освобождения от внешней функции, или, сославшись на единственность степени с данным основанием и данным показателем. Но в рамках текущей статьи нас интересует решение уравнения методом возведения его обеих частей в одну и ту же степень, поэтому, проведем решение именно этим методом.
на основании метода освобождения от внешней функции, или, сославшись на единственность степени с данным основанием и данным показателем. Но в рамках текущей статьи нас интересует решение уравнения методом возведения его обеих частей в одну и ту же степень, поэтому, проведем решение именно этим методом.
Учитывая свойство степени в степени (см. свойства степеней), несложно догадаться, что избавиться от иррациональных показателей позволяет возведение обеих частей уравнения в степень  . Здесь мимоходом заметим, что
. Здесь мимоходом заметим, что  - положительное число (при необходимости смотрите сравнение чисел), и при этом не натуральное. Мы вправе осуществить задуманное возведение частей уравнения в положительную ненатуральную степень, так как степени, находящиеся в левой и правой части исходного уравнения, на ОДЗ для исходного уравнения не принимают отрицательных значений. При этом мы получим равносильное уравнение, что было обосновано в одном из предыдущих пунктов текущей статьи.
- положительное число (при необходимости смотрите сравнение чисел), и при этом не натуральное. Мы вправе осуществить задуманное возведение частей уравнения в положительную ненатуральную степень, так как степени, находящиеся в левой и правой части исходного уравнения, на ОДЗ для исходного уравнения не принимают отрицательных значений. При этом мы получим равносильное уравнение, что было обосновано в одном из предыдущих пунктов текущей статьи.
Итак, проводим возведение обеих частей уравнения  в одну и ту же степень
в одну и ту же степень  . Имеем
. Имеем  . Это уравнение равносильно исходному, значит, решив его, мы будем иметь интересующее нас решение.
. Это уравнение равносильно исходному, значит, решив его, мы будем иметь интересующее нас решение.
Решаем полученное уравнение:

Так мы пришли к кубическому уравнению x3−x2+2=0. Один его корень x=−1 легко подбирается. Разделив многочлен x3−x2+2 на двучлен x+1, получаем возможность представить кубическое уравнение в виде (x+1)·(x2−2·x+2)=0. Квадратное уравнение x2−2·x+2=0 не имеет решений, так как его дискриминант отрицательный. Из этого заключаем, что уравнение x3−x2+2=0 имеет единственный корень x=−1.
В процессе решения мы дважды отмечали, что нам будет необходимо сделать проверку найденных корней. Сейчас пришло это время. Проверку выполним через подстановку найденного корня x=−1 в исходное уравнение  , имеем
, имеем

Ответ:
−1.